La seguridad actual de la autenticación inalámbrica PSK (III)
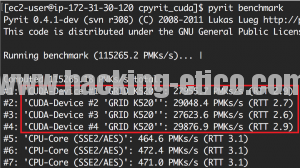
En esta tercera entrega, llega el momento de extraer nuestras propias conclusiones sobre la seguridad actual de la autenticación PSK. Resulta que con la ejecución de Pyrit en una instancia g2.8xlarge del Cloud de Amazon, se obtiene un rendimiento interesante en el cómputo de claves:
Tal y como se puede observar en la ilustración anterior, se cuenta con un cálculo de 115.265 claves/segundo, un incremento más que considerable en referencia a las 836 claves/s iniciales de mi máquina virtual.
Pero esto no termina aquí. Aún podemos mejorar la capcidad de cómputo y de una forma más que considerable. Existen dos opciones:
- Ejecución de Pyrit en modo distribuido.
- Utilizar tablas PMK precomputadas.
Una vez más, debido a la magnitud que debe respetar el artículo, es necesario focalizar nuestros esfuerzos en una de las opciones anteriores y, en este caso, se ha optado por mostrar la velocidad extrema que se consigue con las tablas PMK precomputadas.
Una tabla PMK precomputada no es nada más que un conjunto de claves PMKs que han sido almacenadas después de su correspondiente generación para un SSID concreto y un diccionario de passphrases. El objetivo que persiguen este tipo de tablas es reducir el trabajo de cómputo en simplemente aplicar la función de hash HMAC-SHA1 sobre la PMK y al resto de atributos del handshake (ANonce, SNonce, AP MAC, STA MAC), reduciendo de esta forma la complejidad del cálculo e incrementando espectacularmente la velocidad de procesamiento de las mismas.
Hasta ahora, el mejor rendimiento obtenido es de 115.265 claves/segundo, revelado por la imagen anterior. Pero, ¿Qué rendimiento esperáis de las tablas precomputadas?
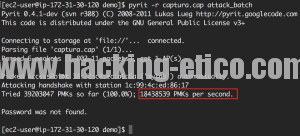
La siguiente ilustración es la respuesta gráfica a la pregunta:
Un total de 18 millones de claves por segundo.
Esto significa que, en un hipotético caso, con el uso de tablas precomputadas y de la ejecución de Pyrit en modo distribuido, sería posible conseguir un total de 1.800 millones de claves por segundo, teóricamente, con 100 máquina distribuidas.
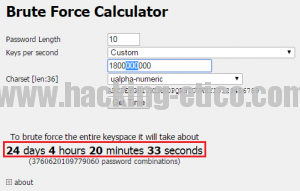
En estas circunstancias, retomando el ejemplo inicial, donde se requieren 143.000 años para una contraseña de 10 caracteres compuesta por mayúsculas y números, a una velocidad de 1.800 millones de claves/segundo proporcionada por 100 instancias, se consigue el siguiente resultado:
Poco más de 24 días para probar todas y cada una de las posibles combinaciones del alfabeto de caracteres especificado y, cabe destacar, que a un coste de 260 $/hora según el precio estipulado en el servicio EC2 de Amazon para el tipo de instancia seleccionado.
Pero ya sabemos que todo no es tan bonito como parece y por desgracia, ha llegado el momento de la desilusión 🙂 . Nada nos impide la ejecución de Pyrit en modo distribuido, pero poder contar con una tabla precomputada de este tipo resulta, prácticamente, imposible. En primer lugar, porque su tamaño es desorbitado (36.577 TB) y también, porque no es una tabla que podamos encontrar y, en consecuencia, la única opción que nos queda es crearla y el tiempo requerido para ello hace que no tenga sentido.
Es necesario recordar que no existe una tabla precomputada que sea «genérica», ya que la PMK se calcula sobre un SSID específico y por lo tanto, sólo es válida para un nombre concreto de red y no puede ser aprovechada por otros.
En cualquier caso, la siguiente imagen emplea una sentencia de Pyrit que permite generar este tipo de tablas:
La denominada wordlist representa el conjunto de passphrases sobre las cuales se derivan las PMKs, que son almacenadas en el fichero de salida result. Por otro lado, mylab consta como el SSID de la red y passthrough es la sentencia que Pyrit ofrece para especificar esta funcionalidad.
El aspecto más importante a destacar es que, tal y como se puede apreciar en la ilustración anterior, con la creación de la tabla se obtiene un rendimiento real de 116.034 PMKs/segundo y por lo tanto, podemos deducir que para averiguar la passphrase se ahorra tiempo de cálculo cuando se realiza la comprobación directamente, es decir, generar directamente la PMK y seguidamente aplicar el hash para comparar el valor del MIC, en lugar de generar primeramente la tabla y a continuación realizar la comprobación, algo que parece lógico en estas circunstancias.
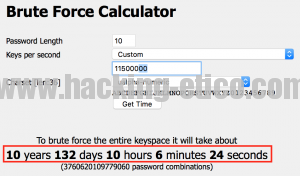
Por lo tanto, si no se trata de un escenario muy especial, la opción de las tablas precomputadas queda descartada. Este hecho nos limita a un rendimiento aproximado de 115.000 PMKs/segundo/instancia, el cual, aplicado nuevamente al ejemplo inicial con un recuento de 100 instancias, deriva a:
Un total de 10 años para probar todas las combinaciones posibles, un tiempo que resulta ser inviable.
De esta forma, las conclusiones que podemos extraer es que un atacante debe recorrer a la aplicación de un ataque dirigido, o también a un ataque estadístico, si quiere tener posibilidades reales de obtener la passphrase, ya que un ataque de búsqueda exhaustiva no es factible.
Por lo tanto, en el sentido inverso, es necesario configurar nuestra red con una contraseña de caracteres aleatorios si pretendemos establecer una buena política de seguridad. Además, es especialmente recomendable que esté compuesta por mayúsculas, minúsculas, números y símbolos, con el fin de incrementar considerablemente las posibles combinaciones.
Otro aspecto a destacar, de gran importancia, es que el ataque a la clave PSK es la debilidad más práctica, pero sólo representa un vector de ataque más. No podemos pensar que por disponer de una buena passphrase se está consiguiendo un alto nivel de seguridad de la red inalámbrica, ya que hay otros factores que pueden permitir revelarla en cuestión de minutos.
Por último, perdonad si he dado un caramelo al principio, pero, ¿No es mejor cuando es más emocionante? 🙂
¡Saludos!
Ferran Verdés
Enlaces:
La seguridad actual de la autenticación inalámbrica PSK (I)
La seguridad actual de la autenticación inalámbrica PSK (II)
La seguridad actual de la autenticación inalámbrica PSK (III)